Esența și metodele extrapolării

Cuvântul compus "extrapolare" este compus din două cuvinte simple. Primul în latină sună în plus și înseamnă „afară”, „pentru”, „afară”. Al doilea din aceeași latină sună polire și înseamnă „schimbare”, „îndreptare”, „neted”. În general, extrapolarea poate fi definită ca o valoare în afara a două puncte date. Se consideră o evaluare a ceea ce este extras din fapte cunoscute care extind datele într-o zonă necunoscută pentru a ajunge la rezultatul dorit. Acest concept poate fi atribuit și prezicerii imaginii viitorului, asumându-se adevărul tendințelor prezente și trecute.

Metoda extrapolării presupune că datele sau observațiile în viitor vor continua să fie similare. Astfel, rezultatele viitoare pot fi prezise. Poate fi considerat ca o ipoteză matematică. Extrapolarea folosește datele și faptele unei anumite situații și oferă predicții despre ce se poate întâmpla până la urmă.

Istoricul extrapolării

Această metodă este adesea denumită extrapolare Richardson sau metoda Romberg. Dar acest lucru nu este complet corect, deoarece de secole există metode numerice similare pentru rezolvarea unor astfel de probleme. Prin urmare, celebrul Richardson h2 (extrapolare pentru o soluție numerică) nu este primul. O metodă similară a fost aplicabilă în calculele Huygens încă din 1654. Termenul „extrapolare” în sine a fost inventat pentru prima dată de Thomas D. Clareson în 1959 într-o carte despre știință și ficțiune.

Metodele de extrapolare pot fi înțelese ca extensii de date sau procese, ceea ce sugerează că un proces similar va fi aplicat în afara lor. Extrapolarea este un concept important folosit nu numai în matematică, ci și în alte domenii, cum ar fi sociologia, psihologia, prognoza. De exemplu, un șofer de obicei extrapolează condițiile de conducere în afara vederii sale. Extrapolarea poate fi atribuită unei metode în care valorile datelor sunt considerate puncte x1, x2 ..., xn, iar apoi valoarea se apropie de limita unui anumit interval de puncte.

Avantajele utilizării:

1. O metodă simplă de prognoză.
2. Nu sunt necesare multe date.
3. Analitică rapidă și ieftină.

Metoda există în statistici. Dacă se elimină periodic valori, răspunsul se apropie de următorul punct de date. Un exemplu de metodă de extrapolare este prognoza meteo, care examinează fondul datelor și extrapolează modelul prevăzut de viitor. Un exemplu și mai simplu, dacă aveți informații despre duminică, luni și marți, puteți extrapola miercuri sau joi.

Dezavantaje ale utilizării extrapolării:

1. Fiabilitate, dacă există fluctuații semnificative în datele istorice.
2. Presupunerea că tendința trecută va continua în viitor este cu greu posibilă în multe medii de afaceri competitive.
3. Ignoră factorii de calitate, cum ar fi schimbările gusturilor și modei.

Accelerarea secvențelor

Metodele de extrapolare sunt de a crea o linie tangentă la sfârșitul datelor cunoscute și de a o extinde dincolo de această zonă. La fel ca interpolarea, extrapolarea folosește multe metode care necesită cunoașterea prealabilă a procesului care creează punctele de date existente. Metoda include extrapolare liniară și polinomială, conică și extrapolare curbă franceză.

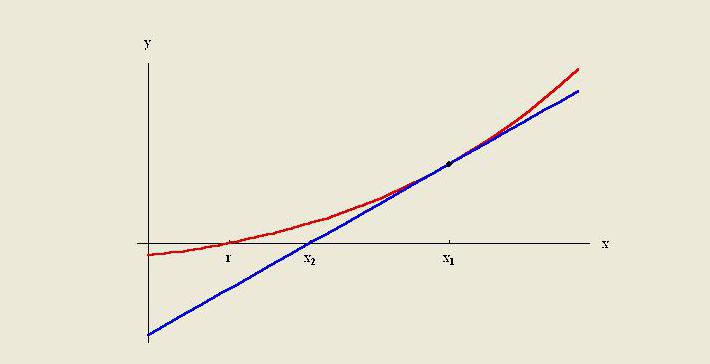
De regulă, calitatea unei anumite metode este limitată de presupuneri despre funcție. În analiza numerică, extrapolarea Richardson este o metodă de accelerare a secvenței, utilizată pentru a îmbunătăți rata de convergență.Se numește după Lewis Fry Richardson. El a introdus tehnica de calcul la începutul secolului XX, a cărei utilitate pentru calcule practice poate fi greu supraevaluată.

Aplicațiile practice ale extrapolării Richardson includ integrarea Romberg, care o aplică la regula trapezului și algoritmul Bulliers-Stoehr pentru a rezolva ecuațiile diferențiale obișnuite.

Metoda liniară

Metoda extrapolării liniare este utilă atunci când este specificată o funcție liniară. Aceasta se realizează prin trasarea unei linii tangente la punctul final al unui grafic dat și extinderea acesteia dincolo. Această metodă de extrapolare în previziune dă rezultate bune atunci când punctul de previzionat nu este prea departe de date. Interpolarea liniară este utilă pentru a găsi valori între punctele date. Poate fi considerat ca „completarea lacunelor” din tabelul de date.

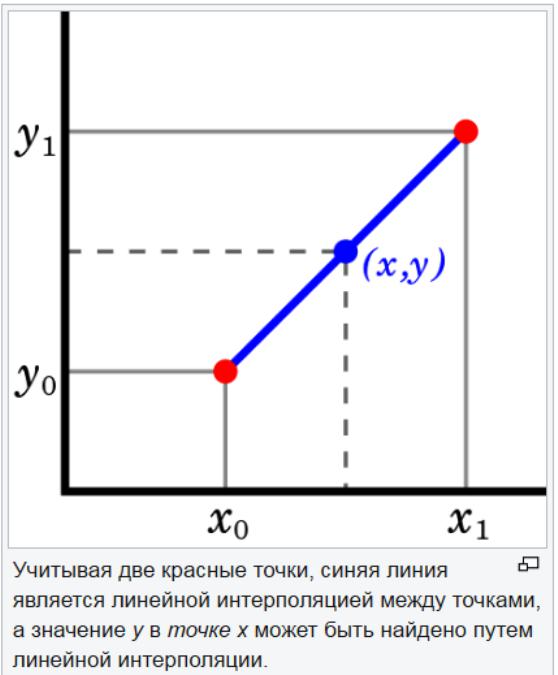
O strategie de interpolare liniară este utilizarea unei linii drepte pentru a conecta puncte de valori cunoscute de o parte și de alta a necunoscutului. Interpolarea liniară nu este exactă pentru parametrii neliniari. Dacă punctele din setul de date se modifică cu o cantitate mare, interpolarea liniară poate oferi o estimare incorectă.

Extrapolarea liniară poate ajuta la estimarea valorilor mai mari sau mai mici decât valorile din setul de date. Strategia sa este de a utiliza un subset de date în loc de întregul set. Pentru acest tip de valoare, este util să se aplice metoda extrapolării în prognoză folosind ultimele două sau trei puncte pentru a estima o valoare care depășește intervalul de date.

Extrapolări polinomiale și conice

Se știe că trei puncte dau un polinom unic. O curbă polinomială poate fi continuată după sfârșitul acestor date. De obicei este efectuată prin metoda Newton cu o diferență finită sau folosind formula de interpolare Lagrange. Un polinom de ordin superior ar trebui extrapolat cu atenția cuvenită, deoarece există șanse corecte de eroare cu extrapolarea polinomială. Dacă se întâmplă acest lucru, estimarea erorii va crește exponențial cu gradul polinomului.

În matematică, extrapolarea polinomială minimă este o transformare de secvență folosită pentru a accelera convergența. Deși metoda lui Aitken este cea mai cunoscută, de multe ori eșuează, în special pentru secvențele vectoriale. În acest caz, se realizează o iterație care construiește matricea. Coloanele sale sunt diferențe.

De exemplu, o metodă de extrapolare pentru o secțiune conică poate fi realizată folosind 5 puncte indicate lângă sfârșitul datelor. În cazul în care secțiunea conică este un cerc sau o elipsă, atunci se va bucla înapoi și se va reuni cu ea însăși. Parabola sau hiperbola nu se intersectează niciodată. Dar ele pot fi îndoite în jurul axei X. Extrapolarea conului se poate face pe hârtie cu o secțiune conică sau folosind un computer.

Metoda evaluării matematice

În această metodă de extrapolare, se prevede valoarea pentru perioada de bază. Acțiunile descrise mai jos sunt efectuate automat de sistem și nu sunt vizibile pentru utilizator. Descrierea este destinată să rafineze algoritmul, care afișează valorile așteptate din cantitatea stocată în sistem și prezice rezultatul măsurării contorului.

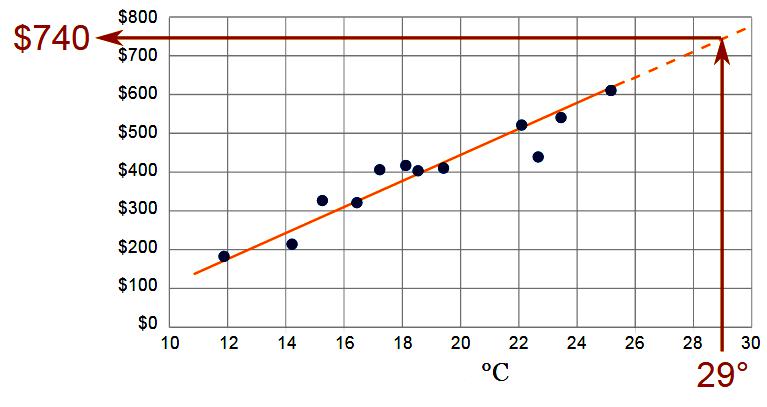
Extrapolarea folosind definiția cantității procedurii se realizează cu ajutorul funcției: Yt = f (yi, t, aj).

Ca bază pentru extrapolare, se adaugă datele rotunjite ale unei perioade de bază tipice stocate în rezultatele lecturii. Sistemul determină greutatea Yt a datelor seriei de timp în t (timpul perioadei de prognoză) pentru a obține soluția corectă prin extrapolare. Unde la punctul de referință se ia yi - nivelul seriei și aj - parametrul ecuației tendinței.

Prezicerea caracteristicilor

Metoda de fixare a unei curbe statistice este aplicabilă predicției funcționalității.Procedurile statistice corespund datelor anterioare ale uneia sau mai multor funcții matematice, cum ar fi liniare, logaritmice, Fourier sau exponențiale. Cele mai bune sunt selectate printr-un test statistic. Atunci această prognoză este extrapolată din această conexiune matematică prin metoda extrapolării matematice. Una dintre cele mai simple modalități de a obține estimări grosolane ale condițiilor viitoare (sau trecute) este extrapolarea datelor care se schimbă în timp.

De exemplu, dacă trebuie să faceți o evaluare bruscă a nivelurilor viitoare de poluanți din apa potabilă cu 20 de ani în avans, puteți extrapola această tendință din ultimii 20 de ani. La fel se observă dacă în viitor, trebuie să estimați prevalența fumatului sau a cancerului pulmonar. Se poate face o prognoză prin calcularea tendințelor din ultimii ani. Extrapolările de acest tip se pot face folosind metode mai puțin complexe. În multe cazuri (în special în domeniile marketingului și managementului afacerilor), metoda de extrapolare este folosită în mod tradițional, de exemplu, prin vizualizarea ultimelor date și evaluarea intuitivă a ceea ce se înțelege în viitor.

Metodele bazate pe reguli pot fi, de asemenea, utilizate prin aplicarea unui set de principii sau așteptări predefinite bazate pe o înțelegere preliminară a sistemului și luând în considerare cele mai recente date pentru interpretarea evenimentelor viitoare.

Cu orice metodă de extrapolare, prudența este importantă datorită prezenței a numeroase incertitudini. Orice procedură de extrapolare se bazează pe presupunerea că informații fiabile sunt disponibile în datele și cunoștințele anterioare. În consecință, viitorul este determinat de aceiași factori care au acționat anterior.

Erori de prognoză

Eșecul extrapolării (mai precis, falia extrapolării nejustificate) apare atunci când fenomenul responsabil pentru o serie de efecte locale banale este citit ca mari fenomene globale. Un alt motiv al erorii este că uneori regulile generalizate sunt deduse din prea puține fapte. Astfel, teoria evoluției lui Darwin este un exemplu fantastic de aplicare a metodei de extrapolare, în care sunt anunțate mecanismele schimbărilor aleatorii și ale selecției naturale care să țină seama de dezvoltarea unor structuri complexe precum viziunea mamiferului sau sistemul imunitar al organismelor vii.

Atunci când încearcă să interpreteze rezultatele cercetării, omul de știință ar trebui să evite extrapolarea în afara domeniului de date și să fie conștient de presupunerile care stau la baza pentru a evita acceptarea concluziilor nevalide. În general, extrapolarea este un instrument științific legitim. Există două aspecte care ajută la distingerea între extrapolarea validă și eronată. Probabilitatea unei extrapolări eronate este mai mare atunci când au fost obținute puncte pentru date insuficiente pentru construcția sa.

Instrumente statistice Excel

Pentru a găsi o corelație între ani și rezultate (de exemplu, într-o afacere), puteți utiliza Excel.

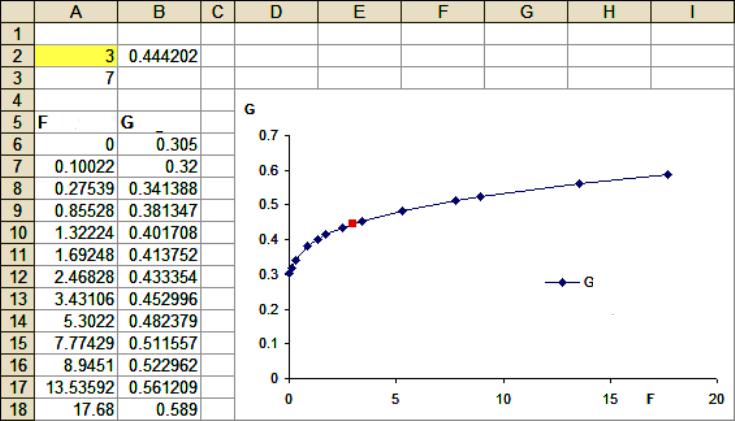
Pentru aceste sarcini, sunt utilizate instrumente statistice pentru modelarea extrapolării care sunt încorporate în toate versiunile Excel, începând cu 97. Procedură:

1. Introduceți valori cunoscute, de exemplu, vânzări totale pentru 2016-2017, dacă trebuie să le determinați pentru 2018 și 2020.
2. Install Analysis, caracteristică care necesită utilizarea unui add-in.
3. Pentru a o instala, extrageți din meniul „Instrumente”, „Adaosuri”.
4. Verificați fereastra utilității de analiză și confirmați cu „OK”.
5. Măsurați corelațiile dintre două serii.
6. Extrapolarea care trebuie făcută are sens numai dacă există o tendință clară (corelație) între cele două seturi de numere (ani și vânzări) prin metoda extrapolării tendințelor.
7. Pentru a măsura această corelație, utilizați meniul „Instrumente”, „Utilități de analiză”.
8. În lista „Instrumente de analiză” selectați „Analiza corelației” și faceți clic pe „OK”.
9. În câmpul Interval de intrare, introduceți intervalul analizat, de exemplu A6: B18, Excel va adăuga simbolul „$”.
10. În zona „Opțiuni de ieșire”, verificați intervalul de ieșire și introduceți-l în câmpul alăturat.
11. Confirmați cu OK.
12. Excel creează o serie de două rânduri în două coloane. Găsiți valoarea calculată (de exemplu, 0,981). Deoarece această valoare este aproape de 1, aceasta înseamnă că există o corelație puternică între ani și cifrele de vânzări. Dacă utilizatorul primește o valoare apropiată de zero, aceasta înseamnă că tendința nu se produce. În acest caz, extrapolarea nu are sens.
13. Începe o evaluare a valorilor viitoare.
14. Selectați intervalul dorit și faceți clic pe butonul „Expertul grafic”.
15. Selectați un grafic (de exemplu, nori de punct) și faceți clic pe Finish.

Utilizarea mediilor mobile

Aceste două metode de extrapolare implică utilizarea pe scară largă a datelor despre vânzări pentru a prezice viitorul. Valoarea medie în mișcare preia o serie de date și „uniformizează” fluctuațiile în ele. Scopul este extragerea extrema de date de la o perioadă la alta. Mediile mobile sunt adesea calculate trimestrial sau săptămânal. Pentru a prezice valorile viitoare, extrapolarea presupune utilizarea tendințelor stabilite de datele istorice. Principala presupunere a extrapolării este că eșantionul va continua în viitor, cu excepția cazului în care dovezile reale indică altfel. Pentru a înțelege mai detaliat aceste metode, puteți lua în considerare un grafic care arată vânzările de gadgeturi pentru întreprinderile mari din 2012 până în 2015.

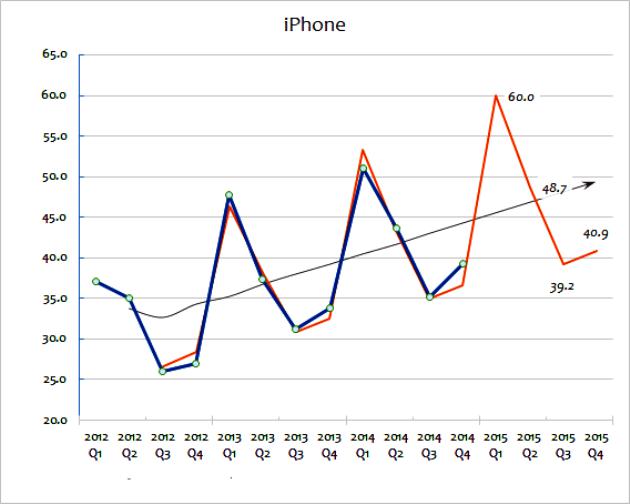
Această metodă de extrapolare a calculului arată cifra de vânzări reală. După cum puteți vedea, suma totală a vânzărilor variază de la an la an, deși puteți ghici (analizând datele) că există o tendință generală de creștere a vânzărilor. Linia neagră arată media în mișcare. Aceasta se calculează adăugând ultimii ani de vânzări (de exemplu Q1 + Q2 + Q3 + Q4) și apoi împărțind la patru.

Această metodă elimină schimbările anuale și oferă o idee bună despre tendința generală a vânzărilor anuale. O medie mobilă ajută la indicarea unei tendințe de creștere, exprimată în procente. Această extrapolare este cea care va fi folosită mai întâi pentru a prezice calea vânzărilor viitoare. Acest lucru poate fi realizat matematic folosind o foaie de calcul. În mod alternativ, o tendință extrapolată poate fi desenată pur și simplu pe un grafic ca o estimare brută.

Corelarea tendințelor

Întotdeauna o tehnologie este înaintarea alteia. Acest lucru se întâmplă atunci când progresele înregistrate în tehnologia precursorului pot fi adoptate de tehnologia adeptă. Atunci când există astfel de relații, cunoașterea schimbărilor în tehnologia predecesorilor poate fi folosită pentru a prezice în viitor evoluția adepților tehnologiei. În plus, extrapolarea precursorului permite predicția continuării urmării dincolo de întârziere.

În acest caz, se utilizează metoda extrapolării tendințelor, în care, de exemplu, sunt comparate tendințele de viteză a aeronavelor militare și de transport. Un alt exemplu de previziune a corelațiilor de tendințe este prezicerea dimensiunii și puterii computerelor viitoare bazate pe progresele tehnologiei microelectronice. Uneori, tehnologia adepților depinde de mai multe tehnologii ale precursorilor, dar nu de un predecesor.

Combinațiile fixe de predecesori pot afecta schimbarea secvenței, dar mai des combinațiile nu sunt fixe, iar intrările predecesorilor diferă atât în ​​combinație, cât și în forță. De exemplu, o creștere a vitezei aeronavei poate apărea datorită îmbunătățirii motoarelor, materialelor, comenzilor, combustibilului, aerodinamicii și a diferitelor combinații ale acestor factori.

Un exemplu de prognoză de corelație obținută prin extrapolarea tendințelor: mile totale de pasageri, mile geografice totale și putere medie de aterizare.Extrapolarea tendințelor determinate statistic permite o abordare obiectivă a prognozei. Cu toate acestea, această abordare are limitări grave și capcane. Orice erori sau alegeri incorecte făcute în determinarea datelor istorice vor fi reflectate în prognoză, ceea ce reduce valoarea acestora.

Aplicații, atribute și limite

Metoda de extrapolare aparține câmpului de prognoză. El sugerează că tiparele care au existat în trecut vor continua în viitor și că aceste tipare sunt regulate și pot fi măsurate. Cu alte cuvinte, trecutul este un bun indicator al viitorului. Aplicațiile sunt utile pentru dezvoltarea datelor de bază.

Atributele și limitele sunt instrumente de calcul simple și ieftine, precum și modele teoretice complexe.

1. Procesarea datelor - grafice și observații.
2. Cheia este să ai o bază de date bună și să înțelegi structura din cadrul ei.
3. Tehnica este cea mai bună potrivire, raport și așa mai departe.

Procedurile statistice standard temporare nu conduc la o selecție exactă a tendințelor pe care previzorul le poate extrapola cu confort, efectuând prognoza prin extrapolare. În astfel de cazuri, previzorul poate „ajusta” rezultatele statistice cu ajutorul judecății. De asemenea, poate ignora complet statisticile și extrapola întreaga tendință bazată pe judecată.

Prognozele generate în acest fel sunt mai puțin precise decât previziunile statistice, dar nu neapărat nesatisfăcătoare. Un exemplu de astfel de extrapolare a unei tendințe de calitate este prezicerea complexității aeronavei. Încercările de a cuantifica această tendință nu au avut succes. Dar procentul de părți mobile sau reglabile ale aeronavei a fost extrapolat cu frecvența cu care au fost introduse astfel de elemente în trecut. Aceste prognoze erau destul de corecte.

Modificări tehnice specifice nu pot fi prezise în acest fel, dar gradul de schimbare poate. Aceasta oferă materiale de planificare utile, indicând o tendință a comportamentului trecut.